表
表(list)是常见的数据结构。从数学上来说,表是一个有序的元素集合。在C语言的内存中,表储存为分散的节点(node)。每个节点包含有一个元素,以及一个指向下一个(或者上一个)元素的指针。如下图所示:

表: 橙色储存数据,蓝色储存指针
图中的表中有四个节点。第一个节点是头节点(head node),这个节点不用于储存元素,只用于标明表的起始。头节点可以让我们方便的插入或者删除表的第一个元素。整个表中包含有三个元素(5, 2, 15)。每个节点都有一个指针,指向下一个节点。最后一个节点的指针为NULL,我们用“接地”来图示该指针。
表的功能与数组(array)很类似,数组也是有序的元素集合,但数组在内存中为一段连续内存,而表的每个节点占据的内存可以是离散的。在数组中,我们通过跳过固定的内存长度来寻找某个编号的元素。但在表中,我们必须沿着指针联系起的长链,遍历查询元素。此外,数组有固定的大小,表可以根据运行情况插入或者删除节点,动态的更改大小。表插入节点时需要从进程空间的堆中开辟内存空间,用以储存节点。删除节点可以将节点占据的内存归还给进程空间。

删除节点, free释放内存

插入节点,malloc开辟内存
表有多种变种。上面的表中,指针指向是从前向后的,称为单向链表(linked list)。还有双向链表(double-linked list),即每个节点增加一个指向前面一个元素的指针。以及循环链表(tabular list),最后一个元素的指针并不为NULL,而是指向头节点。不同类型的链表有不同的应用场景。
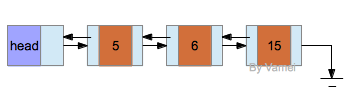
双向链表
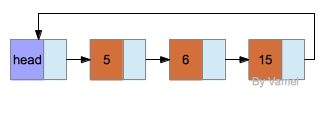
循环链表

双向循环链表
单向链表的C实现
一个数据结构的实现有两方面: 1. 数据结构的内存表达方式; 2. 定义在该数据结构上的操作。我们这里实现最简单的单向链表。表所支持的操作很灵活多样,我们这里定义一些最常见的操作。每个操作都写成一个函数。
/* By Vamei */ #include#include typedef struct node *LIST; typedef struct node *position; /* node,节点 */struct node { int element; position next;};/* * operations (stereotype) * 操作 */ LIST init_list(void);void delete_list(LIST); int is_null(LIST); void insert_node(position, int);void delete_node(LIST, position); position find_last(LIST);position find_value(LIST, int);position find_previous(LIST, position); void print_list(LIST); /* for testing purpose */void main(){ LIST L; position np; int i; /* elements to be put into the list */ int a[] = {1, 3, 5, 7, 9}; /* initiate a list */ L = init_list(); print_list(L); /* insert nodes. Insert just after head node */ for (i=4; i>=0; i--) { insert_node(L, a[i]); } print_list(L); /* delete first node with value 5 */ np = find_value(L, 5); delete_node(L, np); print_list(L); /* delete list */ delete_list(L); /* initiate a list */ L = init_list(); print_list(L); /* insert nodes. Insert just after head node */ for (i=4; i>=0; i--) { insert_node(L, a[i]); } print_list(L); /* delete list */ delete_list(L);}/* * Traverse the list and print each element * 打印表 */void print_list(LIST L){ position np; if(is_null(L)) { printf("Empty List\n\n"); return; } np = L; while(np->next != NULL) { np = np->next; printf("%p: %d \n", np, np->element); } printf("\n");}/* * Initialize a linked list. This list has a head node * head node doesn't store valid element value * 创建表 */LIST init_list(void) { LIST L; L = (position) malloc(sizeof(struct node)); L->next = NULL; return L;}/* * Delete all nodes in a list * 删除表 */void delete_list(LIST L){ position np, next; np = L; do { next = np->next; free(np); np = next; } while(next != NULL); }/* * if a list only has head node, then the list is null. * 判断表是否为空 */int is_null(LIST L) { return ((L->next)==NULL);}/* * insert a node after position np * 在np节点之后,插入节点 */void insert_node(position np, int value) { position nodeAddr; nodeAddr = (position) malloc(sizeof(struct node)); nodeAddr->element = value; nodeAddr->next = np->next; np->next = nodeAddr; }/* * delete node at position np * 删除np节点 */void delete_node(LIST L, position np){ position previous, next; next = np->next; previous = find_previous(L, np); if(previous != NULL) { previous->next = next; free(np); } else { printf("Error: np not in the list"); }}/* * find the last node of the list * 寻找表的最后一个节点 */position find_last(LIST L){ position np; np = L; while(np->next != NULL) { np = np->next; } return np;}/* * This function serves for 2 purposes: * 1. find previous node * 2. return NULL if the position isn't in the list * 寻找npTarget节点前面的节点 */position find_previous(LIST L, position npTarget){ position np; np = L; while (np->next != NULL) { if (np->next == npTarget) return np; np = np->next; } return NULL;}/* * find the first node with specific value * 查询 */position find_value(LIST L, int value) { position np; np = L; while (np->next != NULL) { np = np->next; if (np->element == value) return np; } return NULL;}
在main()函数中,我们初始化表,然后插入(1, 3, 5, 7, 9)。又删除元素5。可以看到,节点零散的分布在内存中。删除节点操作不会影响其他节点的存储位置。
我们随后删除表,又重新创建表。可以看到,这次表占据内存的位置与第一次不同。
下面是main()函数的运行结果。
Empty List
0x154d0b0: 1 0x154d090: 3 0x154d070: 5 0x154d050: 7 0x154d030: 9 0x154d0b0: 1 0x154d090: 3 0x154d050: 7 0x154d030: 9 Empty List0x154d070: 1 0x154d010: 3 0x154d0b0: 5 0x154d090: 7 0x154d050: 9
总结
表: 内存中离散分布的有序节点
插入,删除节点